すーがくをがくすー

中の人は情報通信工学専攻です。専攻がらみの数学・物理（特に院試のネタになりそうなもの）を扱う予定。

〔線形代数〕ジョルダン（Jordan）標準形の理論①（概要編）

　線形代数を習う上では避けては通れない「行列の対角化」。応用的には, この操作により行列の n 乗を一般的に求められたり出来て大変便利である。しかし, すべての行列がみな対角化可能というわけではなく, この事実そのものは初学者のレベルでも理解できる。その局面まで到達すると「対角化不可能な際はジョルダン標準形にする」という知識を得るのだが, ジョルダン標準形への変換方法について述べている文献は数あれど, 理論的な部分まで踏み込むものはやはりそれほど多くはなく, かつ踏み込んでいるものは説明がムズカシスギルことが多いというギャップが存在する。そこで, 備忘録も兼ねて, ジョルダン標準形の理論と実際の操作方法を, いくつかの記事に分けて解説してみることにした。その際, 中の人が工学系の人間であることも踏まえ, 数学的に踏み込みすぎず, かつ理論の要は外さないように心がけてみようと思う。


1.1 ジョルダン標準形とは何か

　ジョルダン標準形とは, 「行列の対角化」によって実現される形の一般化である。例を挙げる。

\displaystyle A = \begin{pmatrix} 0 & 1 & -2 & 2 \\ -1 & 2 & -1 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & -1 & 3 \\ \end{pmatrix}

という行列は, 例えば固有値 1 に対応する固有ベクトル \displaystyle \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \\ \end{pmatrix} および, 固有値 2 に対応する固有ベクトル \displaystyle \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \\ \end{pmatrix} をもつ。対角化のための変換行列 P は1次独立な固有ベクトルを列ベクトルとして並べたものであるが, この場合1次独立な固有ベクトルはこの2本しかない。しかし, P \in \mathbb{R} ^ {4 \times 4} を構成するためには1次独立な列ベクトル4本を必要とするから, 変換行列 P を構成することが出来ない。つまり, 対角化不可能である。

　そこで, 次善の策として, 「対角化の形に最も近い変換」を考えたくなり, その一つがジョルダン標準形である。実際, 例えば

\displaystyle P = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ \end{pmatrix}

に対して,

\displaystyle P ^ {-1} A P = \left ( \begin{array} {cc|cc} 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \hline 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 2 \\ \end{array} \right )

のように, ジョルダン標準形へと相似変換できる（補足1）。

　ジョルダン標準形のポイントは, 対角化不可能な行列を. ジョルダン細胞 J(\lambda, m) \in \mathbb{R} ^ {m \times m} と呼ばれる行列

\displaystyle J(\lambda, m) = \begin{pmatrix} \lambda & 1 & 0 & \cdots & 0 \\ 0 & \lambda & 1 & \cdots & 0\\ 0 & 0 & \lambda & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & 1 \\ 0 & 0 & 0 & \cdots & \lambda \\ \end{pmatrix}

によるブロック対角化行列へと相似変換することである。実際, 先ほどの A は

\displaystyle P ^ {-1} A P = \left ( \begin{array} {cc|cc} J(1, 2) & O \\ O & J(2, 2) \\ \end{array} \right )

と変換されていることが分かる。特に, ジョルダン標準形におけるジョルダン細胞がすべて J(\lambda, 1) \in \mathbb{R} ^ {1 \times 1} のとき, これは「対角化」の操作に一致する。ゆえに, ジョルダン標準形は対角化の一般化と見なすことが出来ることも理解できよう。

　さて, 以下では, ジョルダン標準形への変換を実現するために必要な理論を, ゆっくりと見ていくことにする。なお, 本シリーズでは原則として実行列, 実固有値における議論を行うものとすることを約束しておく。


1.2 広義固有空間（一般化固有空間）の定義

　ジョルダン標準形を学ぶ上で, 大きな役割を果たすのが, 「固有空間」および「広義固有空間（一般化固有空間）」である。ひとまず, 定義を示すことにする。

定義1.2.1　固有空間
　 A \in \mathbb{R} ^ {n \times n} の固有多項式
\displaystyle \varphi _ A (\lambda) = \mathrm{det} (\lambda I - A) \displaystyle = (\lambda - \lambda _ 1) ^ {\nu _ 1} (\lambda - \lambda _ 2) ^ {\nu _ 2} \cdots (\lambda - \lambda _ p) ^ {\nu _ p}
について, E _ A (\lambda _ i) = \mathrm{Ker} (A - \lambda _ i I) を \lambda _ i に対応する固有空間と定義する。 ここで, \lambda _ 1 , \lambda _ 2 , \cdots , \lambda _ p は A の相異なる固有値である。


　これだけ見ると複雑だが, 固有ベクトルが成す空間を新たに明示的に定義しているだけである。つまり, \boldsymbol{x} \in \mathbb{R} ^ n を A の固有値 \lambda _ i に対応する固有ベクトルとすれば,
A \boldsymbol{x} = \lambda _ i \boldsymbol{x} \Longleftrightarrow (A - \lambda _ i I) \boldsymbol{x} = \boldsymbol{0}

\Longleftrightarrow \boldsymbol{x} \in \mathrm{Ker} (A - \lambda _ i I) = E _ A (\lambda _ i)

となる。

　ジョルダン標準形の理論では, これを一般化した, 「広義固有空間」が重要な役割を果たす。この定義も述べておこう。

定義1.2.2　広義固有空間（一般化固有空間）
　 A \in \mathbb{R} ^ {n \times n} の固有多項式
\displaystyle \varphi _ A (\lambda) = \mathrm{det} (\lambda I - A) \displaystyle = (\lambda - \lambda _ 1) ^ {\nu _ 1} (\lambda - \lambda _ 2) ^ {\nu _ 2} \cdots (\lambda - \lambda _ p) ^ {\nu _ p}
について, F _ A (\lambda _ i) = \mathrm{Ker} (A - \lambda _ i I) ^ {\nu _ i} を \lambda _ i に対応する広義固有空間（一般化固有空間）と定義する。


　気持ちとしては, 「広義固有空間に含まれる任意の一般化固有ベクトル \boldsymbol{x} は, 1回 (A - \lambda _ i I) を作用させた（乗じた）だけではゼロにならないかもしれないが, 少なくとも \nu _ i 回作用させれば必ずゼロになる」ということを意味する。ここで, 1回作用させれば消えるものが特に「固有ベクトル」である。つまり, E _ A (\lambda _ i ) \subseteq F _ A (\lambda _ i) である。


1.3 ジョルダン標準形の存在を保証するための重要な定理

　ジョルダン標準形の非常におおまかな流れを得るためには, 最低限以下の3つの定理を用意すれば十分である。

定理1.3.1　広義固有空間の A 不変性
　広義固有空間 F _ A (\lambda _ i) は A 不変である。すなわち, \forall \boldsymbol{x} \in F _ A (\lambda _ i) に対して A \boldsymbol{x} \in F _ A (\lambda _ i) である。


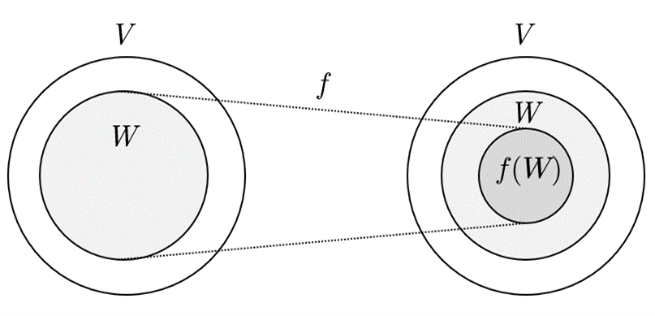
　この定理のイメージを以下に示そう。一般に, 不変部分空間とは, 部分空間 W に線形写像 f を作用させたとき, 生成される空間 f(W) が元々の部分空間 W を「はみ出さないような」部分空間 W を意味している。

不変部分空間

定理1.3.2　広義固有空間による直和分解
　 A \in \mathbb{R} ^ {n \times n} における広義固有空間 F _ A (\lambda _ i) により, 全体空間は
\displaystyle \mathbb{R} ^ n = F _ A (\lambda _ 1) \oplus F _ A (\lambda _ 2) \oplus \cdots \oplus F _ A (\lambda _ p) \tag{1.3.1} と直和分解できる。


　

　まず, 「直和分解」について述べておこう。ある線形空間が直和に分解できる, とは「その線形空間を, 互いに非ゼロ元を一切共有しないような部分空間の和で（綺麗に分割して）過不足無く表せる」ということである。例えば, 3次元ユークリッド空間は, x 軸上のベクトルを元にもつ線形空間, y 軸上のベクトルを元にもつ線形空間, z 軸上のベクトルを元にもつ線形空間の直和で表せる。詳しくは別途調べて欲しい。

　この定理の意味するところはなにか。これを直感的に理解するためには, 対角化可能な行列に対する対角化の操作を思い出すと良い。例えば,

\displaystyle B = \begin{pmatrix} 3 & 1 & 1 \\ 2 & 4 & 2 \\ 1 & 1 & 3 \\ \end{pmatrix} \in \mathbb{R} ^ {3 \times 3}

は対角化できて,

\displaystyle \begin{pmatrix} -1 \\ 1 \\ 0 \\ \end{pmatrix} , \begin{pmatrix} -1 \\ 0 \\ 1 \\ \end{pmatrix} \in E _ A (2) , \quad \begin{pmatrix} 1 \\ 2 \\ 1 \\ \end{pmatrix} \in E _ A (6)

という3つの1次独立な固有ベクトルを得ることが出来る。これらが1次独立であるということは, 全体空間 \mathbb{R} ^ 3 をこれらのベクトルの1次結合で表現できることを意味し, さらに \mathbb{R} ^ 3 = E _ B (2) \oplus E _ B (6) まで言える, ということもイメージは出来よう（厳密な議論はたやすくないかもしれないが）。

　次に A の例を見てみよう。1.1で確認したように, A は対角化不可能であり, それは1次独立な固有ベクトルが2本しか集まらず, 2本足りなかったためであることも既に確認した。 \mathrm{dim} \, E _ A (1) + \mathrm{dim} \, E _ A (2) = 2 \lt 4 であるから, 明らかに E _ A (1) \oplus E _ A (2) = \mathbb{R} ^ 4 も達成できない。しかし, 広義固有空間 F _ A (\lambda _ i) は 固有空間 E _A (\lambda _ i) を含むような, より大きな部分空間であり, 広義固有空間を用意すれば F _ A (1) \oplus F _ A (2) = \mathbb{R} ^ 4 が達成できる, ということを意味している。


定理1.3.3　広義固有空間の次元
　 A \in \mathbb{R} ^ {n \times n} における広義固有空間 F _ A (\lambda _ i) は,
\displaystyle \mathrm{dim} \, F _ A (\lambda _ i) = \nu _ i \tag{1.3.2} を満たす。


　この定理の気持ちを述べる。まず, 定理1.3.2から, 直和と同値な条件として

\mathrm{dim} \, F _ A (\lambda _ 1) + \mathrm{dim} \, F _ A (\lambda _ 2) + \cdots + \mathrm{dim} \, F _ A (\lambda _ p) = n \tag{1.3.3}

を得る。

　一方, 固有多項式の定義より,

\displaystyle \varphi _ A (\lambda) = \mathrm{det} (\lambda I - A)

\displaystyle = (\lambda - \lambda _ 1) ^ {\nu _ 1} (\lambda - \lambda _ 2) ^ {\nu _ 2} \cdots (\lambda - \lambda _ p) ^ {\nu _ p}

であった。当然, 固有多項式の次数は n だから,

\nu _ 1 + \nu _ 2 + \cdots + \nu _ p = n \tag{1.3.4}

である。 (1.3.3), (1.3.4) を比較すれば, (1.3.2) が成立していて欲しいと考えるのは自然で, そしてそれは実際に成立する。
　

　これらの定理の証明は次回の記事に回すとして, とりあえずこれらの定理を押さえれば, ジョルダン標準形の実現に一歩近づくことができるところを, 次節にて示そう。


1.4 ジョルダン標準形定理の極めて大雑把な「気持ち」

　定理1.3.1, 1.3.2, 1.3.3を認めた上で, ジョルダン標準形定理の「気持ち」を先に述べて, 今後の見通しを良くしておこう。まず, 一般化固有空間 F _ A (\lambda _ i) の次元は定理1.3.3より \nu _ i だったから, F _ A (\lambda _ i) の基底を \{ \boldsymbol{x} _ 1 ^{(i)}, \boldsymbol{x} _ 2 ^{(i)}, \cdots, \boldsymbol{x} _ {\nu _ i} ^{(i)} \} と定めると, F _ A (\lambda _ 1) , F _ A (\lambda _ 2), \cdots , F _ A (\lambda _ p) に関する基底をすべて集めた

\left \{ \boldsymbol{x} _ 1 ^{(1)}, \cdots, \boldsymbol{x} _ {\nu _ 1} ^{(i)}, \boldsymbol{x} _ 1 ^{(2)}, \cdots, \boldsymbol{x} _ {\nu _ 2} ^{(2)}, \cdots , \cdots , \boldsymbol{x} _ 1 ^{(p)}, \cdots, \boldsymbol{x} _ {\nu _ p} ^{(p)} \right \}


は, 定理1.3.2より全体空間 \mathbb{R} ^ n の基底を成す。故に, これらの基底のすべてを列ベクトルにもつ P \in \mathbb{R} ^ {n \times n} は正則である。

　さて, F _ A (\lambda _ i) = \mathrm{span} \, \{ \boldsymbol{x} _ 1 ^{(i)}, \cdots, \boldsymbol{x} _ {\nu _ i} ^{(i)} \} は A 不変部分空間であったから（つまり F _ A (\lambda _ i) の任意の元 \boldsymbol{x} について, A \boldsymbol{x} が F _ A (\lambda _ i) の基底の1次結合で表せるから）, F _ A (\lambda _ i) における基底 P _ i = \left ( \boldsymbol{x} _ 1 ^{(i)}, \cdots, \boldsymbol{x} _ {\nu _ i} ^{(i)} \right ) \in \mathbb{R} ^ {n \times \nu _ i} に関する, 行列 A による線形写像の適当な表現行列 A _ i を定めることが出来て, \displaystyle A P _ i = P _ i A _ i とすることができる。

　いま, P = (P _ 1 , P _ 2 , \cdots , P _ p) であったから,

\displaystyle AP = P \begin{pmatrix} A _ 1 & O & \cdots & O \\ O & A _ 2 & \cdots & O \\ \vdots & \vdots & \ddots & \vdots \\ O & O & \cdots & A _ p \\ \end{pmatrix} \tag{1.4.1}

とブロック対角行列に相似変換可能である。特に, p = n すなわちすべての固有値が異なるとき, すべての A _ i が 1 \times 1 の正方行列であり, 対角化を得ることが出来る。


　これから先考えていくのは, 各 F _ A (\lambda _ i) の基底 \{ \boldsymbol{x} _ 1 ^{(i)}, \boldsymbol{x} _ 2 ^{(i)}, \cdots, \boldsymbol{x} _ {\nu _ i} ^{(i)} \} を「うまく」定めれば, ジョルダン細胞を用いて

\displaystyle A _ i = \begin{pmatrix} J(\lambda _ i, \cdot) & O & \cdots & O \\ O & J(\lambda _ i, \cdot) & \cdots & O \\ \vdots & \vdots & \ddots & \vdots \\ O & O & \cdots & J(\lambda _ i, \cdot) \\ \end{pmatrix} \tag{1.4.2}

が実現できることであり, また, その定め方である。このときの基底の定め方を議論すれば, 冒頭にあげたジョルダン標準形が, (1.4.1), (1.4.2) から実現できる。

（つづく）


補足1. 相似について

　 A, A' \in \mathbb{R} ^ {n \times n} に対し, 正則な T \in \mathbb{R} ^ {n \times n} が存在して

\displaystyle A' = T ^ {-1} A T

が成立するとき, A, A' は相似である, という。

〔確率論〕逆関数法による確率分布の生成

　区間 [ 0, 1 ] 上の一様分布に従う確率変数 X から, 任意の確率分布（に従う乱数）を生成する逆関数法を, 定理を覚えることなく使用するための手法について, 問題を通して扱ってみる。


（問題）

問　題

　区間 [ 0, 1 ] 上の一様分布に従う確率変数 X から, 確率密度関数

\displaystyle p(x) = \frac{2}{\pi (e ^ x + e ^ {-x})} \tag{1} 　

に従う確率変数 f(X) を生成する。このとき, f を定めよ。



（概観）

　個人的に確率論・統計論は「門戸が広く, 奥も深い」というイメージを持っている。確率変数一つとっても, その厳密な定義にはルベーグ積分に端を発する測度論に踏み込まなければならず, 「掴めた！」という感覚を得にくい分野の一つだろう。あくまで確率に全く精通していない個人の主観だが。

　さて, まずは本問の意味するところを, p(x) の累積分布関数を F(x) = P(Y \leq x) とし, 数式に置き換えてみる（ここで, 与えられた密度関数 p(x) に従う確率変数を Y としている）。すると, 本問は

\displaystyle P(f(X) \leq a) = F(a) \tag{2}

が成立するような関数 f を定めよ, と述べている。


　次に, (2) の左辺に注目しよう。いま, X の従う確率分布は [ 0, 1 ] 上の一様分布, と明確に与えられている。であれば, (2) の左辺の ( ) の内部において, X が陽に現れるようにうまく変形したい。そこで, f(X) \leq a において両辺 f の逆関数を作用させることを考える。


　しかし, 安易に両辺逆関数をとるわけにはいかない。なぜなら, 不等号の向きがどうなるかに関する議論が必要となるからだ。あるいは, 逆関数そのものの存在が言えるかどうかも分かっていない。

　ここで大きく効いてくるのは, 一般論として, 関数 f が「（連続な）単調増加関数」であるとき, （厳密な証明は省略するが）

「（ f が単調増加） ⇒ （ f^{-1} が存在）」

「（ f が単調増加） ⇒ （ f^{-1} が単調増加）」

がどちらも保証される, という事実である。これは以下の図を見ればほぼほぼ明らかであろう。

単調増加関数

本問において, これらの成立は非常に都合が良い。そこで, f が単調増加関数であるという仮定のもと, 両辺の逆関数をとってみる。すると, 以下のようになる。

\displaystyle P(X \leq f ^ {-1} (a)) = F(a) \tag{3}

　 X が区間 [ 0, 1 ] 上の一様分布に従うという仮定から, 左辺の値はそのまま f ^ {-1} (a) となる。ということは, f の逆関数の形が分かったので, f = F ^ {-1} が言えるのである。最後に, 実際に F が累積分布関数であるという仮定から, F ^ {-1} が存在して, かつそれが単調増加関数である。よって, f に課した「単調増加関数」という仮定は適当であったことも分かる。


　以上に留意すれば, 逆関数法の定理を忘れてしまっても, 以下の解答のようにしていちから f を生成することが出来るだろう。

（解答）

[1]　与えられた密度関数の累積分布を求める

　　 p(x) の累積分布関数 F(x) を求める。定義より,

\displaystyle F(x) = \int _ {- \infty} ^ {x} p(t) dt
\displaystyle = \frac{2}{\pi} \int _ {- \infty} ^ {x} \frac{1}{e ^ t + e ^ {-t}} dt
\displaystyle = \frac{2}{\pi} \int _ {0} ^ {e ^ x} \frac{1}{u + \frac{1}{u}} \frac{du}{u} （ u = e ^ t と変数変換）
\displaystyle = \frac{2}{\pi} \int _ {0} ^ {e ^ x} \frac{1}{u ^ 2 + 1} du
\displaystyle = \frac{2}{\pi} \left [ \arctan {u} \right ] _ {0} ^ {e ^ x}
\displaystyle = \frac{2}{\pi} \arctan {(e ^ x)}

　を得る。

[2]　問題文の言い換え

　　さて, 題意より,

\displaystyle P \left( f(X) \leq a \right) = \frac{2}{\pi} \arctan {(e ^ a)} \tag{4}

　を満たす f を求めればよい。

[3]　求める関数の単調増加性を仮定

　　ここで, f が単調増加であると仮定する。このとき f は逆関数をもち, かつその逆関数は単調増加である。よって, f(X) \leq a \Longleftrightarrow X \leq f ^ {-1} (a) だから,

\displaystyle P \left( X \leq f ^ {-1} (a) \right) = \frac{2}{\pi} \arctan {(e ^ a)} \tag{5}

　を満たす f を求める問題に帰着される。


[4]　求める関数を累積分布関数 F で表す

　　 (5) において, いま X が一様分布に従うという仮定から, P(X \leq x) = x となるので,

\displaystyle f ^ {-1} (a) = \frac{2}{\pi} \arctan {(e ^ a)} \tag{6}

　となる。


[5]　求める関数を得る

　　 (6) より, 求める f を得る。 \displaystyle y = \frac{2}{\pi} \arctan{e ^ x} とおくと,

\displaystyle \frac{\pi}{2} y = \arctan(e ^ x)

\displaystyle e ^ x = \tan \left ( \frac{\pi}{2} y \right )

\displaystyle x = \log _ {e} \left ( \tan \left ( \frac{\pi}{2} y \right ) \right ) \Longleftrightarrow y ^ {-1} = \log _ {e} \left ( \tan \left ( \frac{\pi}{2} x \right ) \right )

　だから, 求める f は

\displaystyle f(x) = \log _ {e} \left ( \tan \left ( \frac{\pi}{2} x \right ) \right )

　となる。これは f が単調増加という仮定を満たす。□


（問題出典・参考文献）

渡辺 澄夫, 村田 昇.『確率と統計 ― 情報学への架橋 ―』. コロナ社.

〔線形代数〕（実）2次形式の最大値問題

　実2次形式とは, \boldsymbol{x} = (x _ 1 , x _ 2 , \dots , x _ n) ^ \top \in \mathbb{R} ^ n ,実対称行列 A \in \mathbb{R} ^ {n \times n} に対して

\displaystyle f(x _ 1, x _ 2, \dots , x _ n) = \boldsymbol{x} ^ \top A \boldsymbol{x}

で表される n 変数多項式である。この多項式を n 変数関数と見て, その最大値を求める手法について, 今回は以下の3つを挙げてみた。

①　対角化の利用

②　ラグランジュの未定乗数法

③　ゴ　リ　押　し

それでは, 順に見ていこう。


（問題）

　問　題

　実 3 変数関数

\displaystyle f(x _ 1 , x _ 2 , x _ 3) = 2 x _ 1 ^ 2 + 2 x _ 2 ^ 2 + 2 x _ 3 ^ 2 + 6 x _ 1 x _ 2 + 8 x _ 2 x _ 3 \tag{1}

における, 制約条件 x _ 1 ^ 2 + x _ 2 ^2 + x _ 3 ^ 2 = 1 のもとでの最大値を求めよ。また, そのときの (x _ 1 , x _ 2, x _ 3) \in \mathbb{R} ^ 3 の値を求めよ。


（解答1）対角化の利用

[1] 議論の流れ

　与えられた関数 f(x _ 1 , x _ 2 , x _ 3) は, 実ベクトル (x _ 1 , x _ 2 , x _ 3) ^ \top \in \mathbb{R} ^ n および 実対称行列 A \in \mathbb{R} ^ {3 \times 3} を用いて

\displaystyle f(x _ 1, x _ 2, x _ 3) = \boldsymbol{x} ^ \top A \boldsymbol{x}, \qquad \boldsymbol{x} = \begin{pmatrix} x _ 1 \\ x _ 2 \\ x _ 3 \end{pmatrix}, A = \begin{pmatrix} 2 & 3 & 0\\ 3 & 2 & 4\\ 0 & 4 & 2 \end{pmatrix}

と表せ, また制約条件は \boldsymbol{x} ^ \top \boldsymbol{x} = 1 と表せる。ここで, A は実対称行列だから, その固有値を \lambda _ 1 \leq \lambda _ 2 \leq \lambda _ 3 とすれば, ある直交行列 P が存在し,

\displaystyle P ^ {\top} A P = \begin{pmatrix} \lambda _ 1 & 0 & 0\\ 0 & \lambda _ 2 & 0\\ 0 & 0 & \lambda _ 3 \end{pmatrix} \Longleftrightarrow A = P \begin{pmatrix} \lambda _ 1 & 0 & 0\\ 0 & \lambda _ 2 & 0\\ 0 & 0 & \lambda _ 3 \end{pmatrix} P ^ {\top}

と対角化できるので,

\displaystyle f(x _ 1, x _ 2, x _ 3) = \boldsymbol{x} ^ \top A \boldsymbol{x} = \boldsymbol{x} ^ \top P \begin{pmatrix} \lambda _ 1 & 0 & 0\\ 0 & \lambda _ 2 & 0\\ 0 & 0 & \lambda _ 3 \end{pmatrix} P ^ {\top} \boldsymbol{x}
\displaystyle = (P ^ {\top} \boldsymbol{x} ) ^ {\top} \begin{pmatrix} \lambda _ 1 & 0 & 0\\ 0 & \lambda _ 2 & 0\\ 0 & 0 & \lambda _ 3 \end{pmatrix} P ^ {\top} \boldsymbol{x}
\displaystyle = \boldsymbol{y} ^ {\top} \begin{pmatrix} \lambda _ 1 & 0 & 0\\ 0 & \lambda _ 2 & 0\\ 0 & 0 & \lambda _ 3 \end{pmatrix} \boldsymbol{y} , \qquad \boldsymbol{y} = P ^ {\top} \boldsymbol{x} = (y _ 1, y_ 2 , y _ 3) ^ \top
= \lambda _ 1 y _ 1 ^ 2 + \lambda _ 2 y _ 2 ^ 2 + \lambda _ 3 y _ 3 ^ 2

と書ける。…①

さらに, 制約条件 \boldsymbol{x} ^ \top \boldsymbol{x} = 1 より , P が直交行列であることに注意して

\displaystyle \boldsymbol{y} ^ \top \boldsymbol{y} = (P ^ {\top} \boldsymbol{x}) P ^ {\top} \boldsymbol{x} = \boldsymbol{x} ^ \top P ^ \top P \boldsymbol{x} = \boldsymbol{x} ^ \top \boldsymbol{x} = 1

を得る。…②

①②および \lambda _ 1 \leq \lambda _ 2 \leq \lambda _ 3 から, f(x _ 1 , x _ 2, x _ 3) \leq \lambda _ 3 を得て, 等号成立は (y _ 1 , y _ 2, y _ 3 ) = (0, 0, 1) であり, つまり \displaystyle \boldsymbol{x} = P(0, 0, 1) ^ {\top} のときである。…③

以上の議論から, A を直交行列 P によって対角化すればよい。


[2] 固有値を得る（対角化 その1）

　　 A の固有多項式（特性多項式） \varphi _ A (\lambda) は, 3次の単位行列を I として

\displaystyle \mathrm{det } (\lambda I - A) = \begin{vmatrix} \lambda - 2 & - 3 & 0\\ -3 & \lambda - 2 & -4\\ 0 & -4 & \lambda - 2 \end{vmatrix} \displaystyle = (\lambda - 2) ^ 3 - 16 (\lambda - 2) - 9 (\lambda - 2) \displaystyle = (\lambda - 2) \left( (\lambda - 2) ^ 2 - 5 ^ 2 \right) \displaystyle =(\lambda + 3) (\lambda - 2) (\lambda - 7)

を得るので, \lambda _ 1 = -3, \lambda _ 2 = 2, \lambda _ 3 = 7 を得る。


[3]　固有ベクトルを得る（対角化 その2）


(a)　 \lambda _ 1 = -3 について

　 A \boldsymbol{v} _ 1 = -3 \boldsymbol{v} _ 1 を満たす \boldsymbol{v} _ 1 を得たい。これは, 言い換えると (A + 3I) \boldsymbol{v} _ 1 = \boldsymbol{0} を得たいので, 固有空間 E _ A (-3) = \mathrm{Ker} \, (A + 3I) の元を求める操作に等しい。

　行基本変形により,

\displaystyle A + 3I = \begin{pmatrix} 5 & 3 & 0\\ 3 & 5 & 4\\ 0 & 4 & 5 \end{pmatrix} \longrightarrow \begin{pmatrix} 5 & 3 & 0\\ 0 & 4 & 5\\ 0 & 0 & 0 \end{pmatrix}

を得るので, \boldsymbol{v} _ 1 = (v _ {11} , v _ {21}, v _ {31})^ \top は

\displaystyle \left\{ \begin{array}{ll} 5 v _ {11} + 3 v _ {21} = 0\\ 4 v _ {21} + 5 v _ {31} = 0 \end{array} \right.


を満たす。正規化すれば,

\displaystyle \boldsymbol{v} _ 1 = \frac{1}{5 \sqrt{2}} \begin{pmatrix} 3\\ -5\\ 4 \end{pmatrix} \in E _ A (-3)

を得る。


(b)　 \lambda _ 2 = 2 について

　同様に,

\displaystyle \boldsymbol{v} _ 2 = \frac{1}{5} \begin{pmatrix} 4\\ 0\\ -3 \end{pmatrix} \in E _ A (2)

を得る。


(c)　 \lambda _ 2 = 7 について

　同様に,

\displaystyle \boldsymbol{v} _ 3 = \frac{1}{5 \sqrt{2}} \begin{pmatrix} 3\\ 5\\ 4 \end{pmatrix} \in E _ A (7)

を得る。


[4]　対角化を実行する（対角化 その3）


　ここまでの議論より,

\displaystyle A ( \boldsymbol{v} _ 1, \boldsymbol{v} _ 2, \boldsymbol{v} _ 3 ) = ( \boldsymbol{v} _ 1, \boldsymbol{v} _ 2, \boldsymbol{v} _ 3 ) \begin{pmatrix} -3 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 7 \end{pmatrix}

だから, 直交行列

\displaystyle P = (\boldsymbol{v} _ 1, \boldsymbol{v} _ 2, \boldsymbol{v} _ 3) = \frac{1}{5 \sqrt{2}} \begin{pmatrix} 3 & 4 \sqrt{2} & 3\\ -5 & 0 & 5\\ 4 & -3 \sqrt{2} & 4 \end{pmatrix}

をとって

A = P \begin{pmatrix} -3 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 7 \end{pmatrix} P ^ {\top}

と対角化できた。


[5]　解答


したがって, ③における議論から, 求める最大値は \lambda _ 3 = 7 であり, このとき

\displaystyle \boldsymbol{x} = \begin{pmatrix} x _ 1\\ x _ 2\\ x _ 3 \end{pmatrix} = P \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} = \begin{pmatrix} \frac{3 \sqrt{2}}{10}\\ \frac{\sqrt{2}}{2}\\ \frac{2 \sqrt{2}}{5} \end{pmatrix}

である。


（解答2）ラグランジュの未定乗数法の利用

制約条件は x _ 1 ^ 2 + x _ 2 ^ 2 + x _ 3 ^ 2 - 1 = 0 だから, g ( x _ 1 , x _ 2, x _ 3) = x _ 1 ^ 2 + x _ 2 ^ 2 + x _ 3 ^ 2 - 1 とおき,

h(x _ 1 , x _ 2 , x _ 3, \lambda) = f (x _ 1 , x _ 2 , x _ 3) - \lambda g (x _ 1 , x _ 2 , x _ 3) \tag{2}

とおく。ラグランジュの未定乗数法によれば, h(x _ 1 , x _ 2 , x _ 3, \lambda) の勾配がゼロとなる点（つまり \nabla h = \boldsymbol{0} となる点）が, 極値の候補を与える。本問において最大値は極値のなかに存在するので, これは最大値の候補を洗い出していることにもなる。

さて,

\displaystyle h(x _ 1 , x _ 2, x _ 3 , \lambda)

\displaystyle = (2 x _ 1 ^ 2 + 2 x _ 2 ^ 2 + 2 x _ 3 ^ 2 + 6 x _ 1 x _ 2 + 8 x _ 2 x _ 3) - \lambda (x _ 1 ^ 2 + x _ 2 ^ 2 + x _ 3 ^ 2 - 1)

\displaystyle = (2 - \lambda) x _ 1 ^ 2 + (2 - \lambda) x _ 2 ^ 2 + (2 - \lambda) x _ 3 ^ 2 + 6 x _ 1 x _ 2 + 8 x _ 2 x _ 3 + \lambda

だから, \nabla h = \boldsymbol{0} となる点, つまり極値の候補は,

\displaystyle \frac{\partial h}{\partial x _ 1} = 0 \Longleftrightarrow 2(2 - \lambda) x _ 1 + 6 x _ 2 = 0　\tag{3}

\displaystyle \frac{\partial h}{\partial x _ 2} = 0 \Longleftrightarrow 2(2 - \lambda) x _ 2 + 6 x _ 1 + 8 x _ 3 = 0　\tag{4}

\displaystyle \frac{\partial h}{\partial x _ 3} = 0 \Longleftrightarrow 2(2 - \lambda) x _ 3 + 8 x _ 2 = 0　\tag{5}

\displaystyle \frac{\partial h}{\partial \lambda} = 0 \Longleftrightarrow x _ 1 ^ 2 + x _ 2 ^ 2 + x _ 3 ^ 2 = 1　\tag{6}

の4つの方程式の解を満たす点 (x _ 1 , x _ 2 , x _ 3) である。

(3) \times x _ 2 と (4) \times x _ 1 から 2(2 - \lambda) を消去することにより,

3 x _ 1 ^ 2 + 4 x _ 1 x _ 3 = 3 x _ 2 ^ 2 \Longleftrightarrow x _ 1 (3 x _ 1 + 4 x _ 3) = x _ 2 \tag{7}

を得る。

同様に, (3), (5) から 2(2 - \lambda) を消去することにより,

3 x _ 2 x _ 3 = 4 x _ 1 x _ 2 \Longleftrightarrow x _ 2 (3 x _ 3 - 4 x _ 1) = 0 \tag{8}

を得る。

　[1]　 x _ 2 = 0 のとき

　　 (7) より

x _ 1 (3 x _ 1 + 4 x _ 3) = 0 \tag{9}


　　(a)　 x _ 1 = 0 のとき

　　　 (6) より x _ 3 = \pm 1 だから,

(x _ 1, x _ 2, x _ 3) = (0, 0, 1), (0, 0, -1) \tag{10}

　

　　を得る。


　　(b)　 x _ 1 \neq 0 のとき

　　　 (7) より 3 x _ 1 + 4 x _ 3 = 0 だから, \displaystyle x _ 1 = - \frac{4}{3} x _ 3 である。

　　　これと (6) より

\displaystyle \frac{16}{9} x _ 3 ^ 2 + x _ 3 ^ 2 = 1 \Longleftrightarrow x _ 3 = \pm \frac{3}{5}

　

　　だから

\displaystyle (x _ 1, x _ 2, x _ 3) = \left( -\frac{4}{5}, 0, \frac{3}{5} \right), \left( \frac{4}{5}, 0, -\frac{3}{5} \right) \tag{11}

　

　　を得る。


　[2]　 x _ 2 \neq 0 のとき

　　 (8) より, 3 x _ 3 - 4 x _ 1 = 0 つまり \displaystyle x _ 3 = \frac{4}{3} x _ 1 を得る。

　　これと (7) より

\displaystyle 3 x _ 1 ^ 2 + 4 \cdot \frac{4}{3} x _ 1 ^ 2 = 3 x _ 2 ^ 2 \Longleftrightarrow x _ 2 = \pm \frac{5}{3} x _ 1

　 を得る。これらを (6) に代入して

\displaystyle x _ 1 ^ 2 + \frac{16}{9} x _ 1 ^ 2 + \frac{25}{9} x _ 1 ^ 2 = 1 \Longleftrightarrow x _ 1 = \pm \frac{3}{5 \sqrt{2}}

　を得る。よって,

\displaystyle (x _ 1, x _ 2, x _ 3) = \left( \frac{3}{5 \sqrt{2}}, \frac{1}{\sqrt{2}}, \frac{4}{5 \sqrt{2}} \right), \left( -\frac{3}{5 \sqrt{2}}, \frac{1}{\sqrt{2}}, - \frac{4}{5 \sqrt{2}} \right),

　

\displaystyle \left( \frac{3}{5 \sqrt{2}}, - \frac{1}{\sqrt{2}}, \frac{4}{5 \sqrt{2}} \right), \left( -\frac{3}{5 \sqrt{2}}, - \frac{1}{\sqrt{2}}, - \frac{4}{5 \sqrt{2}} \right) \tag{12}

　

　を得る。


　ここまでで, 極値の候補が (10),(11), (12) として得られたので, 順に値を f(x _ 1, x _ 2, x _ 3) 代入して, 最大となるものを選べばいい。したがって,

\displaystyle (x _ 1, x _ 2, x _ 3) = \left( \frac{3}{5 \sqrt{2}}, \frac{1}{\sqrt{2}}, \frac{4}{5 \sqrt{2}} \right)

　

のとき, 最大値 7 を得る。□


（解答3）ゴリ押し（参考）

　答えを求めるだけなら以下のような解答もあり得なくはないだろう。原理だけなら高校生でも理解が可能である。

　制約条件 x _ 1 ^ 2 + x _ 2 ^ 2 + x _ 3 ^ 2 = 1 を, 「3次元ユークリッド空間における単位球面上を動く」と見なせば, 球座標系の表現ができる, すなわち

\displaystyle \left\{ \begin{array}{ll} x _ 1 = \sin {\theta} \cos {\varphi}\\ x _ 2 = \sin {\theta} \sin {\varphi}\\ x _ 3 = \cos {\theta} \end{array} \right. \qquad 0 \leq \theta \leq \pi, 0 \leq \varphi \leq 2\pi

と座標変換できる。

　これを代入して整理すると,

\displaystyle f = 2 + \frac{3}{2} \sin {2 \varphi} - \frac{3}{2} \sin {2 \varphi} \cos {2 \theta} + 4 \sin{\varphi} \sin {2 \theta}

を得る。ここで, 三角関数の合成を \sin{2\theta}, \cos{2\theta} について行って,

\displaystyle f = 2 + \frac{3}{2} \sin {2 \varphi} + \sqrt{ \frac{9}{4} \sin ^ 2 {2\varphi} + 16 \sin ^2 {\varphi} } \sin{ (2 \theta + \alpha) }

であり, -1 \leq \sin{(2 \theta + \alpha)} \leq 1 に注意すれば

\displaystyle f \leq 2 + \frac{3}{2} \sin {2 \varphi} + \sqrt{ \frac{9}{4} \sin ^ 2 {2\varphi} + 16 \sin ^2 {\varphi} }

とでき, 変数を無事1つまで絞ることが出来た。

　あとは,

\displaystyle g(\varphi) = 2 + \frac{3}{2} \sin {2 \varphi} + \sqrt{ \frac{9}{4} \sin ^ 2 {2\varphi} + 16 \sin ^2 {\varphi} }
\displaystyle = 2 + 3 \sin {\varphi} \cos{\varphi} + \sqrt{ 9 \sin ^ 2 {\varphi} \cos ^ 2 {\varphi} + 16 \sin ^2 {\varphi} }

の最大値について調べればいい。そこで, x = \sin{\varphi} \in [ -1 , 1 ] とおくと,

\displaystyle g = 2 \pm 3 x \sqrt{1 - x ^ 2} + \sqrt{ 9 x ^ 2 (1 - x ^ 2 ) + 16 x ^ 2 }
\displaystyle = 2 \pm 3 x \sqrt{1 - x ^ 2} + \sqrt{ 25 x ^ 2 - 9 x ^ 4 }

であるが, これの最大値を調べる上では, 結局

\displaystyle h(x) = 2 + 3 x \sqrt{1 - x ^ 2} + \sqrt{ 25 x ^ 2 - 9 x ^ 4 }, \qquad x \in [ 0, 1 ]

の最大値を調べれば十分である。微分して,

\displaystyle h'(x) = 3 \sqrt{1 - x ^ 2} - \frac{3 x ^ 2}{\sqrt{1 - x ^ 2}} + \frac{18 x ^ 2 - 25}{\sqrt{ 25 - 9 x ^ 2 }}

だから, 極値は

\displaystyle 3 \sqrt{1 - x ^ 2} - \frac{3 x ^ 2}{\sqrt{1 - x ^ 2}} + \frac{18 x ^ 2 - 25}{\sqrt{ 25 - 9 x ^ 2 }} = 0

\displaystyle 3 \sqrt{1 - x ^ 2} - \frac{3 x ^ 2}{\sqrt{1 - x ^ 2}} = - \frac{18 x ^ 2 - 25}{\sqrt{ 25 - 9 x ^ 2 } }

を満たす x である。さらに, t = x ^ 2 \in [0, 1] として

\displaystyle 3 \sqrt{1 - t} - \frac{3 t}{\sqrt{1 - t}} = - \frac{18 t - 25}{\sqrt{ 25 - 9 t } }

両辺2乗して

\displaystyle 9(1 - t) - 18t + \frac{9 t ^ 2}{1 - t} = \frac{(18 t - 25) ^ 2}{25 - 9t}

実は, この両辺を整理すると線形方程式

\displaystyle 400 - 544t = 0

に帰着できるので, \displaystyle t = x ^ 2 = \frac{25}{34} で極値をとることがわかり, 実際にこの値を h(x) に代入して, 最大値 \displaystyle h \left( \sqrt{\frac{25}{34}} \right) = 7 を得る。このときの (x _ 1 , x _ 2, x _ 3) については, 煩雑となるので割愛させて頂く。ともあれ, 高校生でも頑張れば求められないことはないのである。

〔ディリクレ積分〕ディリクレ積分の種々の導出法

　工学系の数学で頻出のディリクレ積分

\displaystyle \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx = \frac{\pi}{2}

の導出のうち, 有名なものを解析学（真っ向勝負）・複素解析（王道）・フーリエ変換（天下り）・ラプラス変換（チート）の4種類ピックアップした。


（問題）　ディリクレ積分

（問題）　次の等式を示せ。

\displaystyle I = \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx = \frac{\pi}{2} \tag{1}


（解答1） 微積分（フビニの定理）の利用

\displaystyle \frac{1}{x} = \int _ {0} ^ {\infty} e ^ {-xy} dy

に注意して, \displaystyle I(R) = \int _ {0} ^ {R} \frac{\sin {x}}{x}dx を書き換えると,

\displaystyle \begin{eqnarray} I(R) = \int _ {0} ^ {R} \left( \int _ {0} ^ {\infty} e ^ {-xy} \sin {x} dy \right) dx \tag{2} \end{eqnarray}

ここで, 累次積分 \displaystyle I(R) = \int _ {0} ^ {R} \left( \int _ {0} ^ {\infty} | e ^ {-xy} \sin {x} | dy \right) dx が有限値に収束することを示す（これにより, フビニの定理から (2) において積分の順序交換が許容される）。

\displaystyle I(R) = \int _ {0} ^ {R} \left( \int _ {0} ^ {\infty} | e ^ {-xy} \sin {x} | dy \right) dx

\displaystyle \leq \int _ {0} ^ {R} \left( \int _ {0} ^ {\infty} e ^ {-xy} x dy \right) dx

\displaystyle = \int _ {0} ^ {R} [- e ^ {-y} ] _ 0 ^ {\infty} dx

\displaystyle = \int _ {0} ^ {R} dx

\displaystyle = R \lt \infty

より, I(R) は絶対収束するので, フビニの定理より累次積分の順序交換ができて,

\displaystyle I(R) = \int _ {0} ^ {\infty} \left( \int _ {0} ^ {R} e ^ {-xy} \sin {x} dx \right) dy

\displaystyle = \int _ {0} ^ {\infty} \frac{1}{y ^ 2 + 1} dy - \int _ {0} ^ {\infty} \frac{e^ {Ry}}{y ^ 2 + 1} (\cos {R} + y \sin {R}) dy

を得る（補足1）…①。

以下, これの右辺第2項が, R \to \infty の極限でゼロに収束することを示す。

\displaystyle \int _ {0} ^ {\infty} \frac{e^ {Ry}}{y ^ 2 + 1} (\cos {R} + y \sin {R}) dy

\displaystyle \leq \int _ {0} ^ {\infty} \frac{e ^ {- Ry}}{y^ 2 + 1} \sqrt{y ^ 2 + 1} dy （補足2）

\displaystyle \leq \int _ {0} ^ {\infty} \frac{e ^ {- Ry}}{\sqrt { y^ 2 + 1 } } dy

\displaystyle \leq \int _ {0} ^ {\infty} {e ^ {- Ry}} dy

\displaystyle = \frac{1}{R} \to 0 \qquad (R \to \infty)

より, \displaystyle \lim _ {R \to \infty} \int _ {0} ^ {\infty} \frac{e^ {Ry}}{y ^ 2 + 1} (\cos {R} + y \sin {y}) dy = 0 を得るので, ①より

\displaystyle I = \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx \displaystyle = \lim _ {R \to \infty} I(R) = \int _ {0} ^ {\infty} \frac{1}{y ^ 2 + 1} dy = [ \arctan {x} ] _ {0} ^ {\infty} = \frac{\pi}{2}

を得る。□


（補足）

補足1.（指数関数）×（三角関数）の積分

　同形出現など様々な求め方があるが, 最も手っ取り早いのは

\displaystyle \int _ {0} ^ {R} e^ {-xy} \cdot e ^ {ix} dx = \int _ {0} ^ {R} e^ {(i - y) x} dx = \frac{e ^ {(i - y)R} -1}{i - y}

の虚部をとることだろう。実際, この結果の虚部をとることで

\displaystyle \int _ {0} ^ {R} e ^ {-xy} \sin {x} dx = \mathrm{Im} \ \left( \int _ {0} ^ {R} e^ {-xy} \cdot e ^ {ix} dx \ \right)

\displaystyle = \frac{1 - e ^ {-Ry} \cos R - y e ^{-Ry} \sin R}{y ^ 2 + 1}

を得る。


補足2. シュワルツの不等式

\cos{R} + y \sin{R} = ( \cos{R}, \sin{R} ) \cdot ( 1, y ) のようにベクトルの内積と見てやれば, シュワルツの不等式より \displaystyle ( \cos{R}, \sin{R} ) \cdot ( 1, y ) \leq \left\| \left( \begin{array}{c} \cos{R} \\ \sin{R} \end{array} \right) \right\| \cdot \left\| \left( \begin{array}{c} {1} \\ {y} \end{array} \right) \right\| = \sqrt{y ^ 2 + 1}

を得る。


（解答2） 複素解析（コーシーの積分定理）の利用

　原点以外で正則な複素関数 \displaystyle f(z) = \frac{e ^ {iz}}{z} を図のような原点を含まない周回積分路 C で積分すると, その結果 \displaystyle J = \oint _ {C} f(z) dz は J = 0 となる…①。これは, 「単純閉曲線で囲まれた領域内で複素関数が常に正則であるとき, その閉曲線に沿った複素関数の積分値はゼロになる」というコーシーの積分定理による。

積分路

一方, J は

\displaystyle J = \int _ {\varepsilon} ^ {R} \frac{e ^{ix}}{x} dx + \int _ {C_R} f(z) dz + \int _ {-R} ^ {- \varepsilon} \frac {e ^ {ix}}{x} dx + \int _ {C_{\varepsilon}} f(z) dz

のように積分路ごとに分割できる。

[1] \displaystyle \int _ {\varepsilon} ^ {R} + \int _ {- R} ^ {-\varepsilon} について

\displaystyle \int _ {-R} ^ {- \varepsilon} \frac {e ^ {ix}}{x} dx を変数変換により書き換えることで,

\displaystyle \int _ {\varepsilon} ^ {R} \frac{e ^{ix}}{x} dx + \int _ {-R} ^ {- \varepsilon} \frac {e ^ {ix}}{x} dx

\displaystyle = \int _ {\varepsilon} ^ {R} \frac{e ^ {ix}}{x} dx - \int _ {\varepsilon} ^ {R} \frac {e ^ {-ix}}{x} dx

\displaystyle = \int _ {\varepsilon} ^ {R} \frac{e ^ {ix} - e^ {-ix}}{x} dx

\displaystyle = 2i \int _ {\varepsilon} ^ {R} \frac{\sin {x}}{x} dx

を得る。


[2] \displaystyle \int _ {C_R} について

　こちらの最終目標は R \to \infty のときに積分値がゼロに収束することを示すことである。以下それを示すが, このとき不等式評価がいささか厳しくなることに注意されたい（分子分母の次数の差が1のときと2以上のときでは, 要求される評価精度が変わってくる。後者の場合は |\sin {x}| \leq 1 というガバガバな評価でも良いが, 今回はそうは行かない）

積分路は C_R : z = Re^{i \theta}, \, \theta \in [0, \pi ] であり, このとき dz = iRe^ {i \theta} d \theta だから,

\displaystyle \left| \int _ {C_R} f(z) dz \right|

\displaystyle \leq \int _ {0} ^ {\pi} \frac{ \left| e ^ {iR(\cos {\theta} + i \sin {\theta})} \right| |i R e ^{i \theta}|}{|R e ^ {i\theta}|}d\theta

\displaystyle = \int _ {0} ^ {\pi} e ^ {-R \sin {\theta}} d\theta

\displaystyle = 2 \int _ {0} ^ {\frac{\pi}{2}} e ^ {-R \sin {\theta}} d\theta （対称性より）

\displaystyle \leq 2 \int _ {0} ^ {\frac{\pi}{2}} e ^ {- \frac{2R}{\pi} \theta} d\theta（補足3）

\displaystyle = \frac{\pi (1 - e ^ {-R})}{R} \to 0 \quad (R \to \infty)

より, \displaystyle \lim _ {R \to \infty} \int _ {C_R} f(z) dz = 0 を得る。


[3] \displaystyle \int _ {C_{\varepsilon}} について

こちらは - \pi i という非ゼロ有限値に収束する。これを示す。

積分路は C_{\varepsilon} : z = \varepsilon e^{i \theta}, \, \theta \in [\pi, 0 ] であり, このとき dz = i{\varepsilon}e^ {i \theta} d \theta だから,

\displaystyle \int _ {C_{\varepsilon}} f(z) dz

\displaystyle = \int _ {\pi} ^ {0} \frac{e ^ {i \varepsilon e ^ {i \theta}}}{\varepsilon e ^ {i\theta}} i \varepsilon e ^ {i\theta} d\theta

\displaystyle = -i \int _ {0} ^ {\pi} e ^ {i \varepsilon e ^ {i \theta}} d\theta \to - i \pi \qquad (\varepsilon \to 0)

よって,

\displaystyle J \to 2i \int _ {0} ^ {\infty} \frac{\sin {x}}{x} dx - i \pi \qquad (R \to \infty, \varepsilon \to 0)

を得る。…②


したがって, ①②より

\displaystyle J = 2i \int _ {0} ^ {\infty} \frac{\sin {x}}{x} dx - i \pi = 0 \Longleftrightarrow \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx = \frac{\pi}{2}

を得る。□


（補足）

補足3.　sin (x) の1次関数による不等式評価

　 \displaystyle \left [0, \frac{\pi}{2} \right ] の範囲において, \displaystyle \sin {x} \geq \frac{2}{\pi}x が成立することを用いた。これは以下の図を見れば明らか。

y = sin(x) と y = 2x/pi の大小関係


（解答3） フーリエ解析（矩形波のフーリエ変換）の利用

　天下り的ではあるが, 以下の矩形波 f(x) をフーリエ変換することにより, I を得ることが出来る。

\displaystyle f(x) = \left \{ \begin{array}{ll} 1 \qquad (|x| \leq 1)\\ 0 \qquad (|x| \gt 1) \end{array} \right. \tag{3}

矩形波

　以下では, （曲がりなりにも数学の記事ということもあり）フーリエ変換 \mathcal{F} [ f(x) ] (\omega) および逆フーリエ変換 \mathcal{F}^{-1} [ f(x) ] (\omega) を

\displaystyle F(\omega) = \mathcal{F} [ f(x) ] (\omega) = \frac{1}{\sqrt{2 \pi}} \int _ {-\infty} ^ {\infty} f(x) e ^{- i \omega x} dx \tag{4}

\displaystyle f(x) = \mathcal{F}^{-1} [ f(x) ] (\omega) = \frac{1}{\sqrt{2 \pi}} \int _ {-\infty} ^ {\infty} F(\omega) e ^{ i \omega x} d \omega \tag{5}

（という実用性よりも対称性を意識したもの）として定義する。

　さて, 既に与えた (3) のフーリエ変換を行うことにより,

\displaystyle F(\omega) = \frac{1}{\sqrt{2 \pi}} \int _ {-1} ^ {1} e ^{- i \omega x} dx

\displaystyle = \frac{1}{\sqrt{2 \pi}} \frac{1}{- i \omega} [ e ^{-i \omega x} ] _ {-1} ^ {1}

\displaystyle = \sqrt{\frac{2}{\pi}} \frac{1}{\omega} \frac{e ^ {i\omega} - e ^ {-i \omega}}{2i}

\displaystyle = \sqrt{\frac{2}{\pi}} \frac{\sin{\omega}}{\omega}

というsinc関数を得る。

逆フーリエ変換の定義 (5) より

\displaystyle f(x) = \mathcal{F}^{-1} [ f(x) ] (\omega) = \frac{1}{\sqrt{2 \pi}} \int _ {-\infty} ^ {\infty} F(\omega) e ^{ i \omega x} d \omega

\displaystyle = \frac{1}{\sqrt{2 \pi}} \sqrt{\frac{2}{\pi}} \int _ {-\infty} ^ {\infty} \frac{\sin{\omega}}{\omega} e ^{ i \omega x} d \omega

\displaystyle = \frac{1}{\pi} \int _ {-\infty} ^ {\infty} \frac{\sin{\omega}}{\omega} e ^{ i \omega x} d \omega

この最後の式において, 特に x = 0 とすることにより, f(0) = 1 に注意して

\displaystyle f(0) = \frac{1}{\pi} \int _ {-\infty} ^ {\infty} \frac{\sin{\omega}}{\omega} d \omega \Longleftrightarrow \pi = \int _ {-\infty} ^ {\infty} \frac{\sin{\omega}}{\omega} d \omega

を得るので, 偶奇性から

\displaystyle \pi = 2 \int _ {0} ^ {\infty} \frac{\sin{\omega}}{\omega} d \omega \Longleftrightarrow I = \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx = \frac{\pi}{2}

を得る。□


（解答4） ラプラス変換の利用

最後に, ラプラス変換 \displaystyle F(s) = \mathcal{L} [ f(x) ] (s) = \int _ {0} ^ {\infty} f(x) e^{-sx} dx を用いたほぼチートのような導出を示す。

定積分 \displaystyle \int _ {0} ^ {\infty} \frac{\sin {tx}}{x} dx を t の関数と見て f(t) とおく。 f(t) をラプラス変換すると, ラプラス変換の線形性より

\displaystyle F(s) = \mathcal{L} \left [ \int _ {0} ^ {\infty} \frac{\sin {tx}}{x} dx \right ] (s) = \int _ {0} ^ {\infty} \mathcal{L} \left [ \frac{\sin {tx}}{x} \right ] (s) dx

\displaystyle = \int _ {0} ^ {\infty} \frac{x}{s ^ 2 + x ^ 2} \cdot \frac{1}{x} dx = \int _ {0} ^ {\infty} \frac{1}{s ^ 2 + x ^ 2} dx

\displaystyle = \frac{1}{s} \left [ \arctan \frac{x}{s} \right ] _ {0} ^ {\infty} = \frac{\pi}{2s}

ここで求めた F(s) を逆ラプラス変換することにより, \displaystyle \mathcal{L} [ 1 ] (s) = \frac{1}{s} に注意して

\displaystyle f(t) = \mathcal{L} ^ {-1} \left [ \frac{\pi}{2s} \right ] (t) = \frac{\pi}{2} つまり \displaystyle \int _ {0} ^ {\infty} \frac{\sin {tx}}{x} dx = \frac{\pi}{2}

を得て, 特に t = 1 として

\displaystyle I = \int _ {0} ^ {\infty} \frac{\sin{x}}{x} dx = \frac{\pi}{2}

を得る。□


参考文献

[1] 海老原 円, 太田雅人. 『詳解と演習 大学院入試問題 〈数学〉』. 数理工学社.

[2] 千葉 逸人. 『新装版 工学部で学ぶ数学』. プレアデス出版.

[3] 八木厚志, 森田浩. 『工学系の数学解析』. 大阪大学出版会.

〔複素解析〕留数定理の実積分への応用①

最近「留数定理気持ちよすぎだろ！」という動画にお目にかかったので, 次の積分を考えてさらに留数定理で気持ちよくなろうと思う。

（問題）

問題：次の I_n の値を求めよ。

\displaystyle I_n = \int_{- \infty}^ {\infty} \frac{1}{x^ {2n} + 1} dx \qquad (n=1, 2, ...)


（方針）

例えば, n = 1 のときは,
\displaystyle I_1 = \int_{- \infty}^ {\infty} \dfrac{1}{x^ {2} + 1} dx = [\arctan{x} ] _ {- \infty}^ {\infty} = \frac{\pi}{2} - \left(- \frac{\pi}{2}\right) = \pi
となるが, これを正攻法で一般化するのは骨が折れる。そこで, 留数定理の出番である。

複素関数

\displaystyle f(z) = \frac{1}{z^ {2n} + 1}

を考え, その極のうち, \mathrm{Im \,} z > 0 の範囲に存在するものを求める。これらの留数を求め, その和に 2\pi i を乗じれば, 図のような周回積分路 C について

\displaystyle \oint _ {C} f(z) dz

を求めることが出来る。…①

積分路

一方,

\displaystyle \oint _ {C} f(z) dz = \int _ {- R} ^ {R} \frac{1}{x^ {2n} + 1} dx + \displaystyle \int _ {C_R} f(z) dz

であり, ここで R \to \infty の極限をとれば, 第1項は I_n となり, 第2項はゼロへと収束する。つまり,

\displaystyle \lim _ {R \to \infty} {\oint _ {C} f(z) dz} = \int _ {- \infty} ^ {\infty} \frac{1}{x^ {2n} + 1} dx + 0= I_n

となる。…②

①②より, 結果として直接求積操作を行うことなく所望の値を得る。


（解答）


1. f(z) の極を求める。


　極は z^ {2n} + 1 = 0 の複素数解であるから, 結局 f(z) の極は, \mathbb{C} 平面上における単位円周を, 座標 (1, 0) を含まないように 2n 分割するように配置されることに注意する。よって,

\displaystyle z = e^ {i \frac{2m + 1}{2n}\pi} , \qquad m = 0, 1, ... , 2n - 1

がすべての極であり, 特に \mathrm{Im \,} z > 0 の範囲に存在するものは

\displaystyle z = e^ {i \frac{2m + 1}{2n}\pi} , \qquad m = 0, 1, ... , n - 1

である。

極の例 (n = 4 のとき)


2. f(z) の極を求める。


　一般に, \displaystyle f(z) = \frac{Q(z)}{P(z)} の1位の極 \alpha における留数は

\displaystyle \mathrm{Res}(\alpha) = \frac{Q(\alpha)}{P'(\alpha)}

で与えられる（補足1）。 P(z) = z^ {2n} + 1 より P'(z) = 2n z ^ {2n - 1} だから,

\displaystyle \mathrm{Res} \left(e^ {i \frac{2m + 1}{2n}} \pi \right) = \frac{1}{2n e^{i \frac{(2m + 1)(2n - 1)}{2n}} \pi} = \frac{1}{2n e^{i \frac{2n - 2m - 1}{2n}} \pi}

つまり

\displaystyle \mathrm{Res} \left(e^ {i \frac{2m + 1}{2n}} \pi \right) = \frac{1}{2n} \cdot {e^{i \frac{2m - 2n + 1}{2n}} \pi}

を得る。


3. 留数定理により \displaystyle \oint _ {C} f(z) dz の値を求める。


　さて, 留数定理より

\displaystyle \oint _ {C} f(z) dz = 2 \pi i \cdot \sum _ {m = 0} ^ {n - 1} \frac{1}{2n} \cdot {e^{i \frac{2m - 2n + 1}{2n}} \pi}

\displaystyle = \frac{\pi i}{n} \cdot e ^ {i \frac{1 - 2n}{2n}} \sum _ {m = 0} ^ {n - 1} e ^ {i \frac{m}{n} \pi}

\displaystyle = \frac{\pi i}{n} \cdot e ^ {i \frac{1 - 2n}{2n}} \cdot \frac{1 - e^{i \pi}}{1 - e ^ {i \frac{\pi}{n} }}

\displaystyle = \frac{\pi i}{n} \cdot \frac{2}{ \left( 1 - e ^ {i \frac{\pi}{n} } \right) \left(e ^ {i \frac{2n - 1}{2n} \pi} \right)}

\displaystyle = \frac{\pi }{n} \cdot \frac{1}{ \frac{ e^ {i \frac{2n - 1}{2n} \pi} - e^ {i \frac{2n + 1}{2n} \pi} }{2i} }

\displaystyle = \frac{\pi }{n} \cdot \frac{1}{ \frac{ e^ {i \frac{2n - 1}{2n} \pi} - e^ {- i \frac{2n - 1}{2n} \pi} }{2i} }

\displaystyle = \frac{\pi }{n} \cdot \frac{1}{\sin{\frac{(2n - 1) \pi}{2n}}}

\displaystyle = \frac{\pi }{n} \cdot \frac{1}{\sin{\frac{\pi}{2n}}}

を得る。…③


4. \displaystyle \lim _ {R \to \infty} {\oint _ {C} f(z) dz} = \int _ {- \infty} ^ {\infty} \frac{1}{x^ {2n} + 1} dx + 0= I_n を示す。


一方,

\displaystyle \oint _ {C} f(z) dz = \int _ {- R} ^ {R} \frac{1}{x^ {2n} + 1} dx + \displaystyle \int _ {C_R} f(z) dz

のように積分路が分割できる。以下, 後者について R \to \infty のときゼロとなることを示す（ z^ {2n} のオーダで収束するのでほぼ明らかではあるが）。積分路は C_R : z = R e^ {i \theta}, \, \theta \in [0, \pi] より

\displaystyle \left| \displaystyle \int _ {C_R} f(z) dz \right|

\displaystyle = \left| \displaystyle \int _ {0} ^ {\pi} \frac{iRe^ {i \theta}}{R^ {2n} e ^ {i 2\theta} + 1} d\theta \right| （ dz = iRe^{i \theta} より）

\displaystyle \leq \displaystyle \int _ {0} ^ {\pi} \frac{|R|}{|R^ {2n} e ^ {i 2\theta} + 1|} d\theta

\displaystyle \leq \displaystyle \frac{R}{R^ {2n} - 1} \int _ {0} ^ {\pi} d\theta

\displaystyle \leq \displaystyle \frac{\pi R}{R^ {2n} - 1} \to 0 \quad (R \to \infty)

である。したがって,

\displaystyle \lim _ {R \to \infty} {\oint _ {C} f(z) dz} = \int _ {- \infty} ^ {\infty} \frac{1}{x^ {2n} + 1} dx + 0= I_n

がいえる。…④


5. ③④を比較して結果を得る。


したがって, ③④を比較して

\displaystyle I_n = \frac{\pi }{n} \cdot \frac{1}{\sin{\frac{\pi}{2n}}}

を得る。□


（補足）


補足1

　求める留数に対する極が1位であることから, P(\alpha) = 0 に注意して

\displaystyle \mathrm{Res} (\alpha) = \lim _ {z \to \alpha} \frac{Q(z)}{P(z)}(z - \alpha) = \lim _ {z \to \alpha} \frac{Q(z)}{ \frac {P(z) - P(\alpha)}{z - \alpha}} = \frac{Q(\alpha)}{P'(\alpha)}

を得ている。